41 The derivative 43 Example 49 Define f R → R by f(x) = x2 sin(1/x) if x ̸= 0, 0 if x = 0 Then f is differentiable on R (See Figure 1) It follows from the product and chain rules proved below that f is differentiable at x ̸= 0 with derivative f′(x) = 2xsin 1 x −cos 1 x Moreover, f is differentiable at 0 with f′(0) = 0, since limClick here👆to get an answer to your question ️ If y = f (2x 1/x^2 1 ) and f^'(x) = sin x^2 , then dy/dx = (IIT JEE, 19)Essentially correct, but more complicated than required You make some confusion about k and j, though Suppose x and y are rational solutions of x^2y^2=3^k, with k an odd integer

If F X X X 1 1 Y Then The Value Of F Y Is
If y=f(x)=x+2/x-1 then x is equal to
If y=f(x)=x+2/x-1 then x is equal to-I=1 A i for some integer n If n = 2, then X = A 1 ∪A 2, A 1 and A 2 are closed in X, fA 1 A 1 → Y and fA 2 A 2 → Y are continuous and fA 1(x) = fA 2(x) for every x ∈ A 1∩A 2 Hence, by the pasting lemma, we can construct continuous f0 X → Y such that f0(x) = fA 1(x) if x ∈ A 1 and f0(x) = fA 2(x) if x ∈ A 2 It is clearIf x = 0, y =0 Stepbystep explanation Hi, to obtain the values of the variable y in each case, we have to replace the variable x




9 If Y F X Frac X 2 X 1 Then F Y Is Equal To A X B Frac Y 2 Y 1 C Frac X 1 X 2 Quad Left D Frac Y 1 Y 2 Right
If f0 is a homeomorphism of X with Z, then f X → Y is a topological imbedding (or simply imbedding) of X in Y Example 5 Consider F (−1,1) → R defined by F(x) = x/(1 − x2) Then F is continuous and one to one (since F0(x) = (1x2)/(1−x2)2 ≥ 0) and is continuous on R So F is a homeomorphism (where R has the standard topologyClick here👆to get an answer to your question ️ Let f N→ X f(x) = 4x^2 12x 15 Then, f^1(y) = ?(b) f(x,y) = 2x2 xy2 −2, D= {(x,y) ∈ R2;x2 y2 64} Solution (a) Calculating the partial derivatives gives f x = y 2 √ x − 1, f y = √ x−2y 6 Finding critical points f x = 0, f y = 0 =⇒ (x,y) = (4,4) Note that (4,4) ∈ Dand that f(4,4) = 12 The boundary of Dconsists of
If xy=2 and x−y=1, then what is xy?Solutionput (xy)=v then differentiate both sides with respect to 'x' we get 1dy/dx=dv/dx or, dy/dx=dv/dx—1 this value put in to equation (I), first arranging equation (I) dy/dx= (xy1) (xy—2)/ (xy2) (xy—1) or, dv/dx—1= (v1) (v—2)/ (v2) (v—1) or,dv/dx= (v^2—2vv—2)/ (v^22v—v—2) 1X 1 6=x 2 Then f(x;y) = x1 2Fhas di erent values on P 1 and P 2, so Fseparates points Since Ris compact, the StoneWeierstrass theorem implies that Fis dense in C(R) Alternatively, note that Fincludes all polynomials in (x;y), and the polynomials are dense in C(R), so Fis dense in C(R) 7
ProofLet fK g 2A be a family of convex sets, and let K = \ 2AK Then, for any x;y2 K by de nition of the intersection of a family of sets, x;y2 K for all 2 nd each of these sets is convex Hence for any 2 A;and 2 0;1;(1 )x y2 KDivide \frac{f1}{f}, the coefficient of the x term, by 2 to get \frac{1}{2}\frac{1}{2f} Then add the square of \frac{1}{2}\frac{1}{2f} to both sides of the equationThis is the Solution of Question From RD SHARMA book of CLASS 11 CHAPTER RELATIONS AND FUNCTIONS This Question is also available in R S AGGARWAL book of CLAS



If Y F 2x 1 X 2 1 And F X Sin X 2 Then Dy Dx Sarthaks Econnect Largest Online Education Community



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf
R X f X(x) dx= 1 Alternately, X may be described by its cumulative distribution function (CDF) The CDF of Xis the function F X(x) that gives, for any specified number x∈X, the probability that theIf x = −1, y =1 ;X y = 2 (equation 1) x y = 1 (equation 2) Add the equations for 2x = 3, meaning that x = 3/2 Using x = 3/2 in equation 1 gives y = 1/2 Using x = 3/2 in equation 2 also gives y = 1/2 (3/2)*(1/2) = 3/4 Answer xy = 3/4




A Function Y F X Satisfies The Differential Equation Dy Dx X 2y 2x 0 F 1 1 Then The Value Of F 1 Is




Square 22 2 42 See How To Solve It At Qanda
Given function f(x) =x/(x1) Then f(1/x) = (1/x)/(1/x) 1 f(1/x) = (1/x)/(1 x)/x f(1/x) = (x/x)/(1 x) f(1/x) = 1/(1 x) Hence, f(x) =x/(x1) then f(1/x) = 12 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all xThe total area under f X(x) is 1;




If F X X X 1 1 Y Then The Value Of F Y Is




12x1 T05 01 Inverse Functions 10
94 7 Metric Spaces Then d is a metric on R Nearly all the concepts we discuss for metric spaces are natural generalizations of the corresponding concepts for R with this absolutevalue metric Example 74 Define d R2 ×R2 → R by d(x,y) = √ (x1 −y1)2 (x2 −y2)2 x = (x1,x2), y = (y1,y2)Then d is a metric on R2, called the Euclidean, or ℓ2, metricIt corresponds toBASIC STATISTICS 3 We can then write 9 as i=1 (xi − a)2 = i=1 (xi −x¯)2 i=1 (¯x− a)2 (11) Equation 11 is clearly minimized when a =¯xNow consider part b of theorem 1 Expand the second expression in part b and simplifyY1 n 1 f X(y 1 n) where, f X() is the pdf of X which is given Here are some more examples Example 1 Suppose Xfollows the exponential distribution with = 1 If Y = p X nd the pdf of Y Example 2 Let X ˘N(0;1) If Y = eX nd the pdf of Y Note Y it is said to have a lognormal distribution Example 3 Let Xbe a continuous random variable with




If F X 1 2x 1 Then Show That F F X 2 X 1 2x 3 2s 1 Provided 1 That 2 1 Y Maths Relations And Functions Meritnation Com



2
The partition theorem says that if Bn is a partition of the sample space then EX = X n EXjBnP(Bn) Now suppose that X and Y are discrete RV's If y is in the range of Y then Y = y is a event with nonzero probability, so we can use it as the B in the aboveM 2, and M 3 be metric spaces Let gbe a uniformly continuous function from M 1 into M 2, and let fbe a uniformlyAnswer to If f(x)= g(h(x)), then f'(4) = 5 9 8 4 7 6 3 5 yvalues yvalues 4 h(x) 2 3 8(x) 2 1 1 1 4 5 1 4 5 2 3 xvalues




Notes On Topics Of Algebra Notes



Www Cbsd Org Site Handlers Filedownload Ashx Moduleinstanceid Dataid Filename Applications of integration separation of vars and slope fields Pdf
5k views asked in Class XI Maths by vijay Premium (539 points) If (1i) 2 / 2i = xiy, then find the value of xy complex numbers and quadratic equationsAssuming that f is nonzero, we can rewrite this equation as 1 f(x) 1 f(1 / x) = 1 Making the substitution g(y) = − 1 2 1 f ( ey), we get the functional equation g(y) g( − y) = 0, which simply says that g is odd This equation can be solved, with the initial condition, by setting g(y) = cy for a suitable constant c Answer If x = −2, y =8 ;



If F X 2f 1 X X 2 Then What Is F X Quora




If Fx X X 1 Then Its Inverse F 1x Has An Equa Gauthmath
1 Let y = x 1 x, try now to express x as a function of y We have x 2 − x y 1 = 0 x = y ± y 2 − 4 2 Substitute this value for x in your expression for f f ( y) = ( y ± y 2 − 4 2) 2 ( 2 y ± y 2 − 4) 2 f ( y) = y 2 − 2Figure 1 A plot of the function y = x2 sin(1=x) and a detail near the origin with the parabolas y = x2 shown in red Then fis di erentiable on R (See Figure 1) It follows from the product and chain rules proved below that fis di erentiable at x6= 0 with derivative f0(x) = 2xsin 1 x cos 1 x Moreover, fis di erentiable at 0 with f0(0) = 0F X(x) ≥0 for all values of x∈X 2The rule of total probability holds;



Solved 3 7 3 A Slope Field For A Differential Equation Is Shown In The Figure Above If Y F X Is The 3 Particular Solution To The Differenti Course Hero



If Math F 2x 1 X Math What Is Math F 2 Math Quora
Clearly f(x) =x^2 for x>/=0, and f(x)= x^2 for x0 For y/=0, g(f(x))=sqrt(x^2)=x and f(g(y)) =(sqrt(y))^2 =y, as x>/=0 => y>/=0 If 8 f(x) 6f(1/x) = x 5 and y = x2 f(x) then (dy/dx) at x = – 1 is (a) {(– 1)/(14)} (b) 0 (c) (1/14) (d) none of there Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesSelect a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex Tap for more steps Replace the variable x x with − 2 2 in the expression f ( − 2) = ( − 2) 2 2 ( − 2) − 1 f ( 2) = ( 2) 2 2 ( 2) 1




A If F X X2 1 X Prove That F X F 1 X B If Y F X




If Y F 2x 1 X 2 1 And F X Sinx 2 Then Dy Dx At X 0 Is
Domain RR{1,3} Range RR # To Find the domain Equate the denominator(x^22x3) to zero, then solve the equation for x rarr x^22x3=0 rarr x=((2)sqrt((2)^24*(1)*(3)))/(2*1) rarr x= 12 => x= 1 and x=3 This means that, when x=1 or 3, we have the x^22x3=0 Implying that f(x)=color(red)(x/0) which is undefined Hence, the domain is all real numbers except 11The PDF f X(x) is positivevalued;(b) Pick = 1 Given any >0, pick x>0 such that 3 x2 2 >1 Then d(x 2;x) < but we have d(f(x 2);f(x)) = j(x 2)3 x3j= j 3 x2 2 3 2x 22 3 23 j 3 x2 2 >1 This shows that f(x) = x3 is not uniformly continuous on R 445 Let M 1;



1




No 1 Ify F X R 1 Then F Y Is T No 2 Limit Of Lx 2 At Scholr
If the eccentricity of the hyperbola $\frac {x^2}{a^2}\frac {y^2}{b^2}=1$ is $\frac {5}{4}$ and $2x 3y 6 = 0$ is a focal chord of the hyperbola, then theGiven a function g with this property, we can easily construct a suitable f Just let f ( x) = { g ( x) x ≥ 0 g ( − x) x < 0 If g is additionally continuous then so is f We can find a lot of continuous g Pick a 1 ∈ ( 0, 1), let a 0 = 0 and recursively a n = a n − 2 2 1 for n ≥ 22x2Thenwecanpluginfory to get f(x,y)=f(x)= ±x p 2x2 The boundary's critical points are precisely those values of x for which 0=f0(x)=⌥ 2(x2 1) p 2x2 This is only true when x = ±1 We then find the corresponding values of y and find the extreme points on the boundary are (1,1),(1,1),(1,1), and (1,1) • Alternatively, we could



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf




D 1 E 30 1 Iff X X 2x 1 Then F 2 A Chegg Com
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `2f (x1)f((1x)/x)=x , then f(x)` is If y = sin^1 x/√(1 x^2), then show that (1 x^2)d^2y/dx^2 3xdy/dx y = 0 asked in Mathematics by Samantha ( 3k points) continuity and differntiabilitySolution for If f(x, y) ha then 2y (11) = (1,1) = 3 Select one True O False Q Find the period of f(x) = tan(4x) 2 and sketch its graphChose a scale for the axes that show at A The objective is to find the period of the given trigonometric function and sketch the graph




If F X X X 1 1 Y Then The Value Of F Y Is Youtube
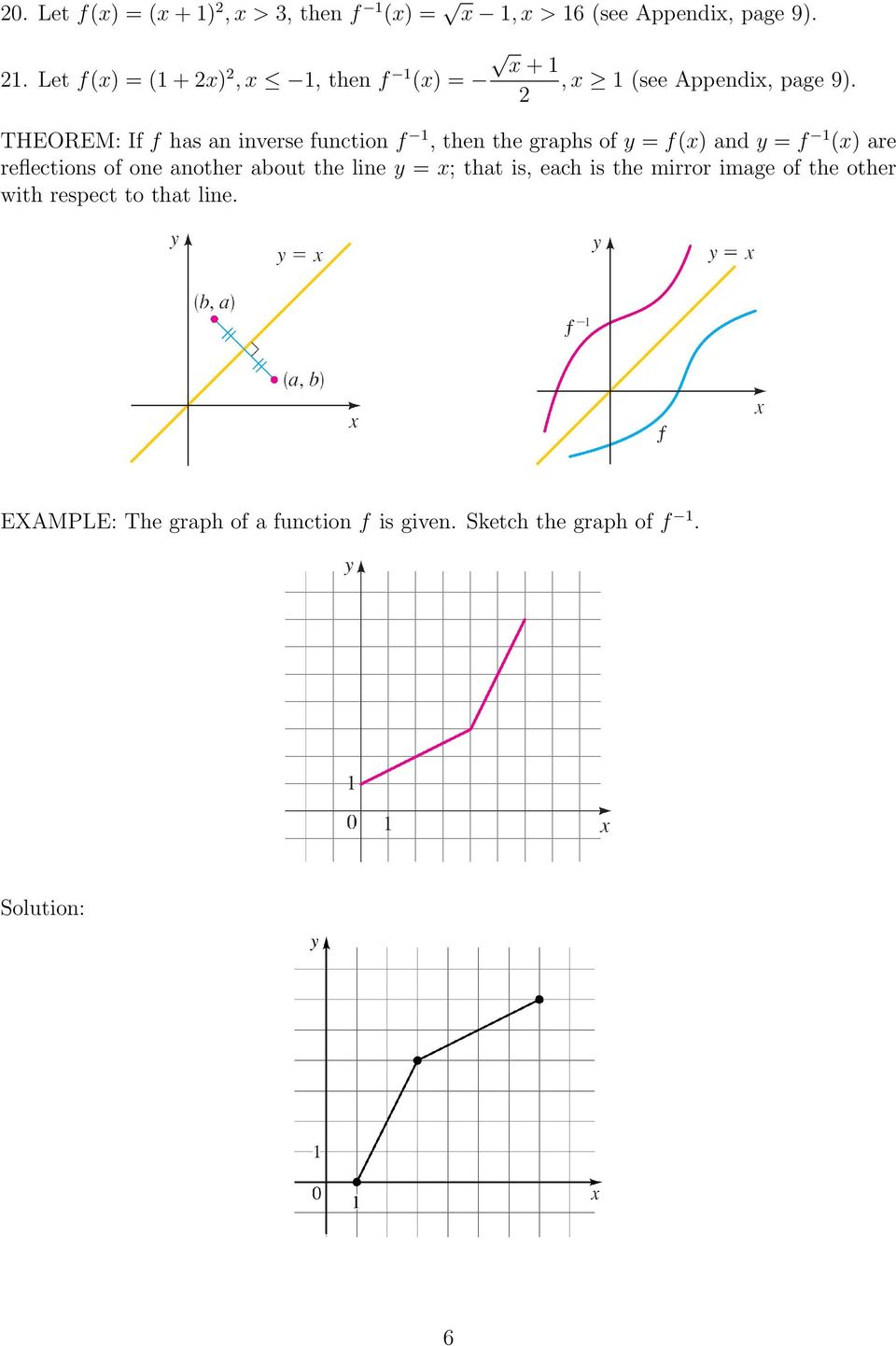



Section 2 7 One To One Functions And Their Inverses Pdf Free Download
If f(x y) = f(x) × f(y) ∀ x, y and f(5) = 2, f '(0) = 3, then f '(5) is (a) 0 (b) 1 (c) 6 (d) 2 Find the set of values of x satisfying sin x cos x = 1, ∀ x ∈ 0, 2πX−y2 − x 6y, D= {(x,y) ∈ R2;0 6x69,0 6y65};Can take y = 2 Then if f(x) = 2x1 = 2, then x = 1/2 ∈/ Z Example 24 Define f Z → Z by f(n) = n5 Show that f is onto Suppose that y ∈ Z is an arbitrary integer We need to show that there exists x ∈ Z such that f(x) = y However take x = y − 5 ∈ Z Then f(x) = x5 = y −55 = y It follows that f is onto 3 OnetoOne Correspondence




Ex 1 2 7 I In Each Of The Following Cases State Whether The




Answered If X Xf Y 1 Then 1 Y 1 Fy Bartleby
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeDefinition X is a continuous random variable if there is a function f(x) so that for any constants a and b, with −∞ ≤ a ≤ b ≤ ∞, P(a ≤ X ≤ b) =Z b a f(x) dx (1) • For δ small, P(a ≤ X ≤ a δ) ≈ f(a) δ • The function f(x) is called the probability density function (pdf) • For any a, P(X = a) = P(a ≤ X ≤ a) =R a a f(x) dx = 0 • A discrete randomPutting x=1y in first equation f (1y)2f (1 1y)= (1y)^22 eq3 Multiply by 2 in eq3 we get 2f (1y)4f (y)=2× (1y)^2 2×2 eq4 Adding eq4 and eq2 we get 3f (y)=y^2 2 2× (1y)^2 4 f (y)= — (3×y^2–4y8)/3 Then put y=x again to have f (x) f (x)= — (3×x^2–4x8)/3



Absolute Value Functions




Calculusstudyguide
If y = (1 1/x2)/(1 1/x2), then dy/dx is Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions toFind if f(t) = 4t\62 t Find dV/dr if V = 4/3 pi r^3 determine whether the statement is true or false Explain your answer If a curve y = f(x) has a horizontal tangent line at x = a, then f'(a) is not defined If the tangent line to the graph of y = f(x) at x = 2 has negative slope, then f'(2) < 0




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib



2



If Y F 2x 1 X 2 1 And F X Sin 2 X Then Dy Dx Sarthaks Econnect Largest Online Education Community




If The Graph Of The Function Y F X Is Symmetrical About The Line X 2 Then Youtube



Www3 Nd Edu Apilking Math Work Old exams Ex1s16solutions Pdf



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




If Y F 2x 1 X 2 1 And F X Sinx 2 Then Dy Dx Is Equal To Youtube




Wbjee Maths Solved Question Paper Download Pdf




If F X X 1x 1 Then F 2x In Terms Of F X Is




Ex 1 3 8 F X X2 4 Show That F Is Invertible Chapter 1



Www Math Utah Edu Gustafso 2250separableeq Pdf




None Is Defective Is 10 If 2x Y 4x 7 7y 13 Then The




Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions
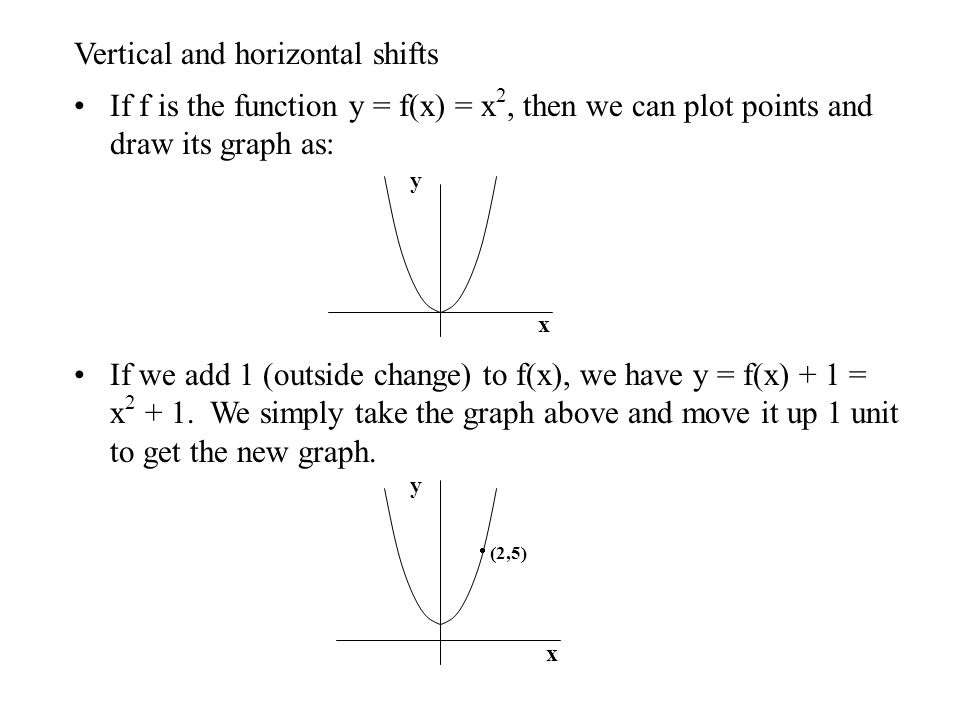



Vertical And Horizontal Shifts If F Is The Function Y F X X 2 Then We Can Plot Points And Draw Its Graph As If We Add 1 Outside Change To




4 If F Is A Function Defined See How To Solve It At Qanda




If Y X 2 5x I E 2x Then Y 2x 5 3 2x Chegg Com




Notes On Topics Of Algebra Notes




If F X A X 1 X A 1 2x Then The Value Of F 0 Is Brainly In




5 If Fx X X 1 Then Its Inverse F 1x Has An Eq Gauthmath




Misc 7 If F X Y F X F Y Such That F 1 3 Find N



Www Liverpool Ac Uk Maryrees Homepagemath191 Diff Pdf




If Y F X X 2 X 1 X Y 1 Then X Is Equal To




81 A Slope Field For A Differential Equation Is Shown In The Figure Above If Y F X Is The Particular Solution To The Differential Equation Through The Point 2 And X 3x F X Then




Solutions To The Extra Sample Questions




Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange




Answered If Y F X Is The Solution Of 18x Y Bartleby




If Y F X Is A Differentiable Function Of X Such That Inverse Function X F 1 Y Exists Then Prove That X Is A Differentiable Function Of Y And Dx Dy 1 Dy Dx Where



If Y F X X 2 X 1 Then A X F Y B F 1 3 C Y Increases With X For X 1 Sarthaks Econnect Largest Online Education Community




Answered 5 Lim V1 T Dt X 1 A 3 B 2 Bartleby




If F Mathbb R Setminus 0 1 To Mathbb R Satisfies F X 2f Left Frac 1 X Right 3f Left Frac X X 1 Right X Then 8f 4 Mathematics Stack Exchange



2




Iit 19 Find Dy Dx If Y F 2x 1 Square X 1 And F X Sin Square X Youtube




12 F X X 1 Then Lim A X B 2x C 2 D 1 E 0 13 Chegg Com




If Y F X 6 E X 1 Then F 1 X Is 1 6 E X 1 Chegg Com



If F X Cos Log X Then F 1 X F 1 X 1 2 F X Y F Xy Is Equal To Sarthaks Econnect Largest Online Education Community



Exercise I Jee Main Hcl Learning Flip Ebook Pages 1 10 Anyflip Anyflip




If F X 2e 2x 2 1 Then F X 2e 4z E 2x 2 1 Chegg Com



If Y Is The Function Of X And Z Ax Then Prove That D 2y Dx 2 A 2d 2y Dz 2 Quora




If F X Sqrt 3x 2 6 And Y F X 3 Then At X 1 Dy Dx Is Equal To Youtube
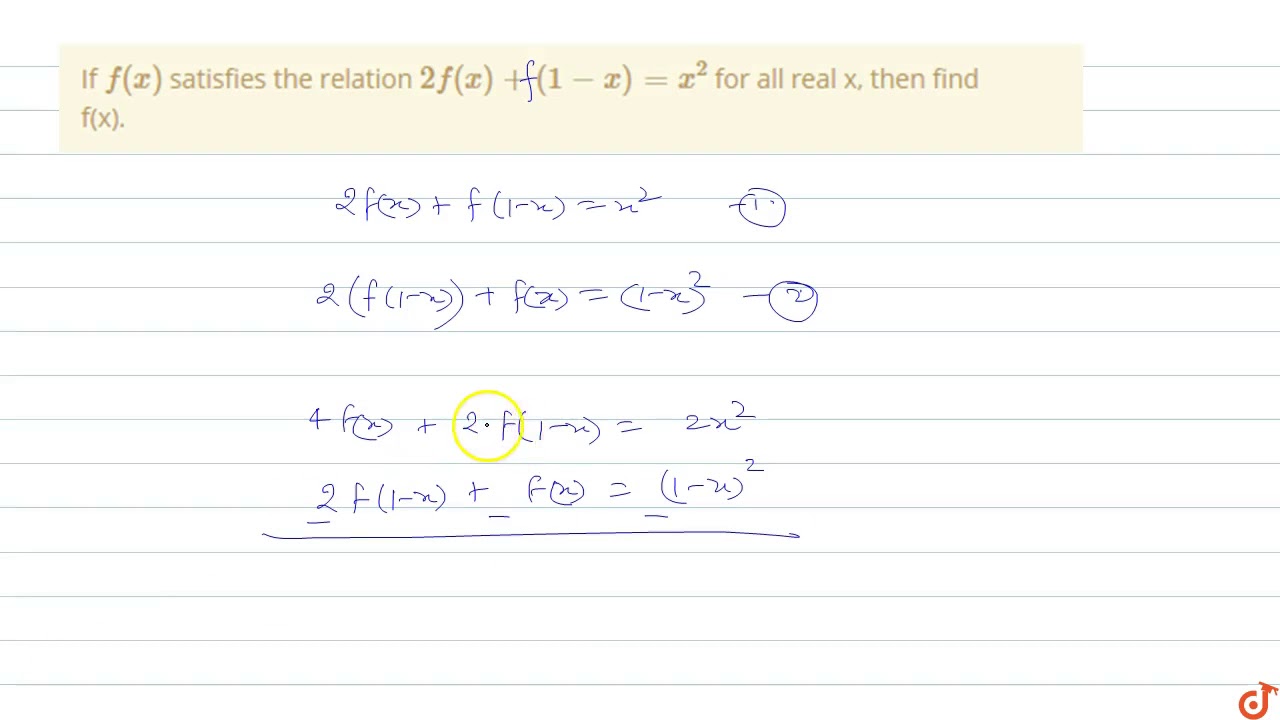



If F X Satisfies The Relation 2f X 1 X X 2 For All Real X Then Find F X Youtube




Vertical And Horizontal Shifts If F Is The Function Y F X X 2 Then We Can Plot Points And Draw Its Graph As If We Add 1 Outside Change To




If F X X 1 X 1 Then F 2x Is Equal To




If F 1 4 And F X Y F X F Y 7xy 4 Then F 2 F 5 Brainly In
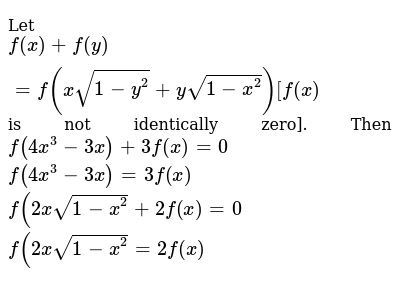



2f X 3f 2x 29 X 2 100 X 80



1




Relations Functions Pps



Solution If Y F X And F X 2x 5 Then The Graph Of Y F X And Y Sqrt F X Will Have Two Common Points One Common Point Is The X Intercept Determine The Other Common Point




If Y F X 2 2 And F 3 5 Then Dydx At X 1 Is




D 1 E 30 1 Iff X X 2x 1 Then F 2 A Chegg Com



Users Math Msu Edu Users Gnagy Teaching 11 Fall Mth234 Mth234 009 E2 F10 Pdf




If F R R Be Defined By F X X 2 1 Then Find F 1 17 And F 1 3



Www Mathcity Org Media Fsc Fsc Part 2 Mcqs Mcqs Math Fsc Part2 Pdf



Www Portnet Org Cms Lib6 Ny Centricity Domain 276 1st and 2nd derivative test 1 Pdf



Case Fiu Edu Mathstat Resources Math Help Math Help Pre Calculus Algebra Assets Lecture Notes Chapter 2 Notes Fall 15 Pdf



If Y 1 T 2 T 2 Where T 1 X 1 Then The Number Of Points Of Discontinuities Of Y F X X R Is Sarthaks Econnect Largest Online Education Community




Given If Y F X 2x 1 3x M And If F Y X Find M Mathematics Topperlearning Com Pghes4dd




Function Mathematics Wikipedia




F X Y 2xe X 2 Y For 0 X 1 And Y X 2 Find The Marginal Density Function Of F Y Mathematics Stack Exchange
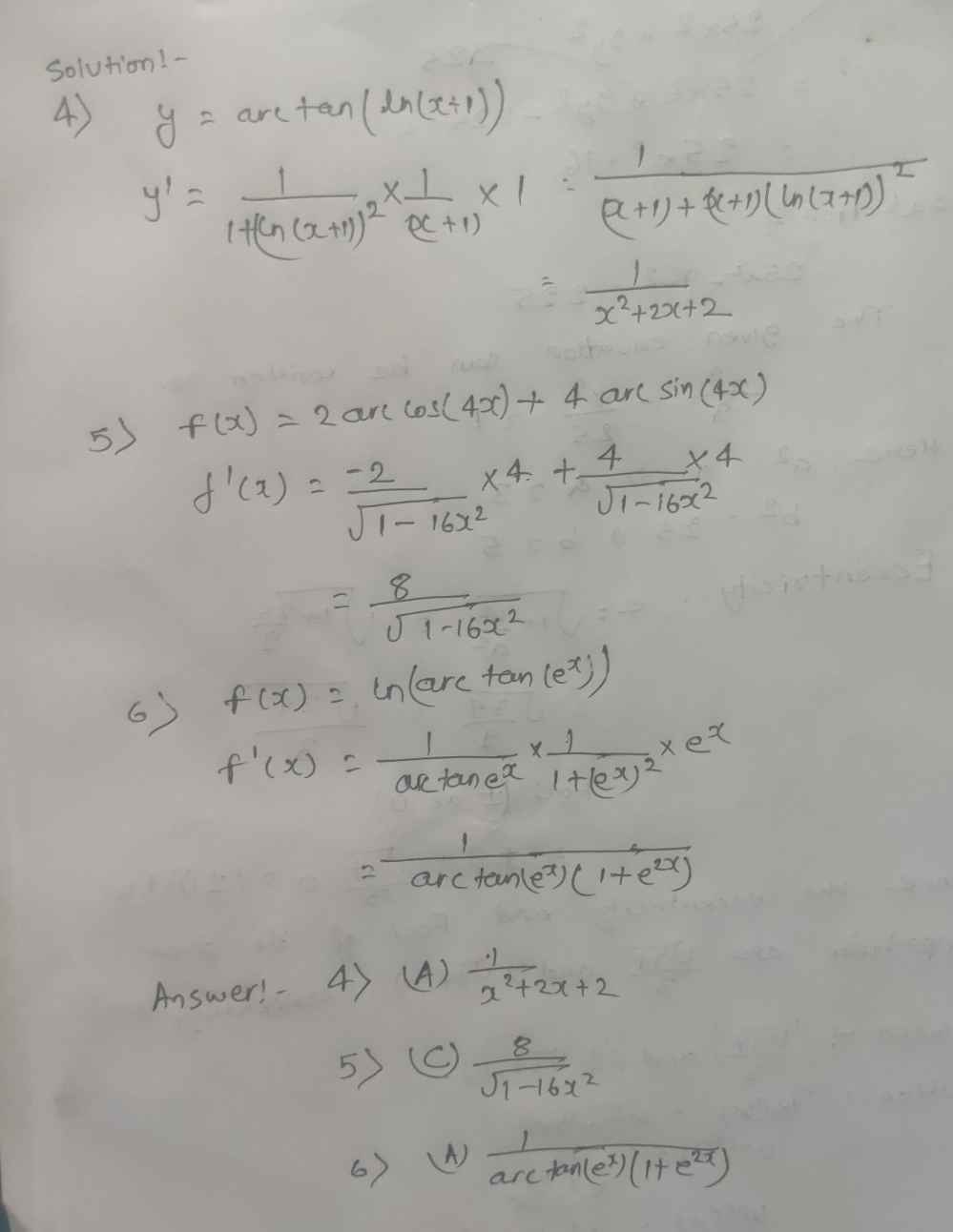



4 If Y Arctan Ln X 1 Then Y Would Be Equal To Gauthmath




Derivative Of Function Of A Function Pdf Mathematical Analysis Derivative




Math1 Lecture Notes 29 Derivatives And Graphs Of Functions 105 29 Derivatives And Graphs Of Functions In This Lecture We Consider The Significance Of The Studocu
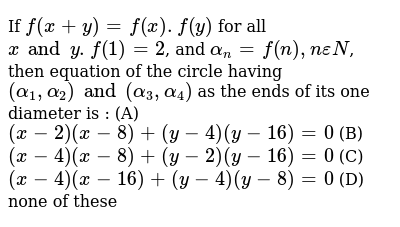



If F X Y F X F Y For All X And Y F 1 2 And Alpha N F N N Epsilon N Then Equation Of The Circle Having Alpha 1 Alpha 2 And Alpha 3 Alpha 4 As The Ends Of




12 F X X 1 Then Lim A X B 2x C 2 D 1 E 0 13 Chegg Com




Logarithms Functions And Other Key Concepts Math 115 Docsity




Let F X Be A Differentiable Function Such That F 0 1 F




9 If Y F X Frac X 2 X 1 Then F Y Is Equal To A X B Frac Y 2 Y 1 C Frac X 1 X 2 Quad Left D Frac Y 1 Y 2 Right




Worksheet 10 Solutions 1 Consider The Function F X 3x4 8x




Differentiation And Application Of Derivative 2 1 Derivative Operator Theory




Chapter Differentiation Questions 1 Find The Value Of Answers 1 2 If F X 2 2x 5 Find F 2 Answers 2 3 If Y 2s And X 2s 1 Ppt Download




If Y F X 1 X 1 X Then Show That X F Y Maths Relations And Functions Meritnation Com




Let Y F X 2x 2 X X 2 X Then Dy Dx F X Find Chegg Com




Fe 9 Suppose The Derivative Of The Function Y F X Chegg Com




Answered Q2 Write True Or False Of The Bartleby




Jee Mains 19 Question Paper With Solutions 9 Jan M1 Kunduz
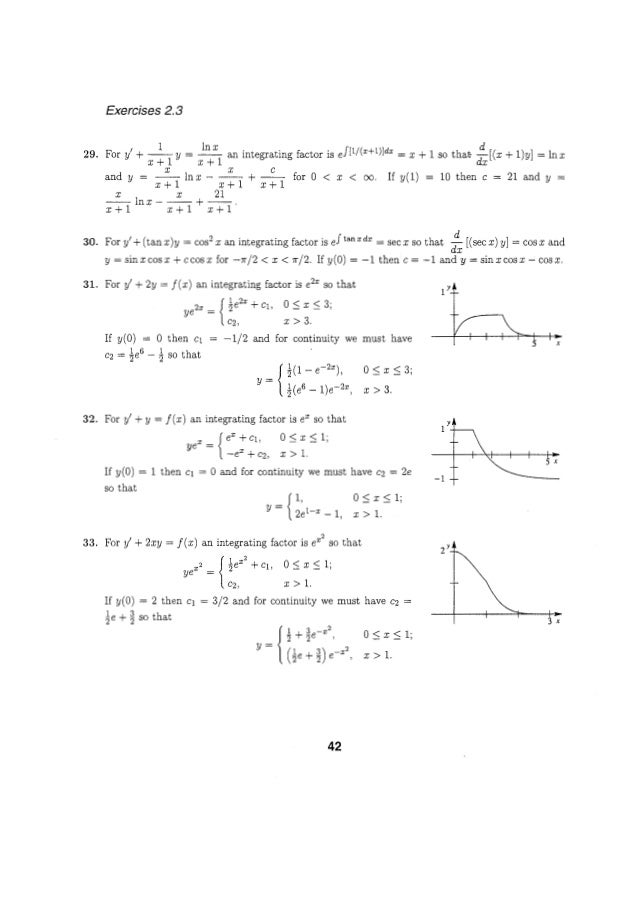



Solucionarioecuacionesdiferencialesdenniszill7aedicion P




Calculusstudyguide



0 件のコメント:
コメントを投稿